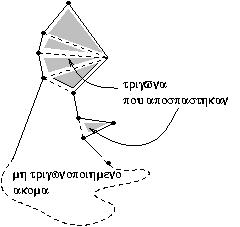
Το java applet παίρνει σαν είσοδο από τον χρήστη με το ποντίκι ένα απλό πολύγωνο το όποιο τριγωνοποιείται με αλγόριθμο που πρώτα το διασπά σε μονότονα πολύγωνα . Κατόπιν τριγωνοποιείται το κάθε ένα από τα μονότονα πολύγωνα δίνοντας μας και την τριγωνοποίηση του απλού πολυγώνου η οποία και εμφανίζεται στο applet οπτίκα.
Απλό πολύγωνο καλείται πέριοχη που περικλείεται από μία κλειστή πολυγωνική αλυσίδα η οποία δεν τέμνει τον ευατό της.
Διαγώνιος καλείται ανοιχτό(δεν περιλαμβάνει τα άκρα του) ευθύγραμμο τμήμα που συνδέει δυο κόρυφες ένος απλού πολυγώνου και κείτεται στο εσωτερικό του απλού πολυγώνου.
Τριγωνοποίση ενός απλού πολυγώνου Π καλούμε την διάσπαση του Π σε τρίγωνα άπο ένα μέγιστο σύνολο ( μη τεμνόμενων μεταξύ τους) διαγωνίων.

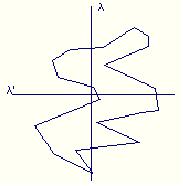
Μονότονο ως πρός μια ευθεία λ καλούμε ένα απλό πολύγωνο Π εφόσον για κάθε ευθεία λ' κάθετη στην λ η τομή του Π με την λ' είναι συνεχής(χώρις κενά). Δηλαδή η τομή θα πρέπει να είναι ευθύγραμμο τμήμα, σημείο , ή κενό. Αν το Π είναι μονότονο ως προς τον άξονα y θα καλείται y-μονότονο. (Μια χαρακτηριστική ιδιότητα ενός y-μονότονου απλού πολυγώνου είναι ότι αν "περπατήσουμε" από την πιο ψηλή κορυφή τους προς την πιο χαμηλή κάτα μήκος της αρίστερης(ή δεξιάς) πλευράς τους τότε πάντα κινούμεστε προς τα κάτω ή οριζόντια , ποτέ προς τα πάνω.
Ο αλγόριθμος που θα χρησιμοποιήσουμε συνίσταται στον χωρισμό πρώτα του απλού πολυγώνου Π σε y-μονότονα κομμάτια , και μετά τριγωνοποίησης του κάθε τέτοιου κομματιού.
Χρησιμόποιουμε αλγόριθμο σάρωσης. 'Εστω κ1,κ2,...,κν μια αριστερόστροφη απαρίθμηση των κορυφών του Π. Έστω ακόμα ε1,ε2,...,εν το σύνολο των ακμών του Π όπου ει = κικι+1 για 1 <= ι <= ν και εν = κνκ1 . Ο αλγόριθμος σάρωσης κινεί μια ιδεατή γραμμή σαρωσής λ προς τα κάτω. Η λ σταματάει σε κάποια σήμεια (γεγονότα) που στην περιπτωσή μας είναι οι κόρυφες του Π. Τα "γεγονότα" αυτά τα κρατούμε σε μια ουρά προτεραιότητας Q , όπου η προτεραιότητα μιας κόρυφης είναι η y συντεταγμένη της. Αν δυο κορυφές έχουν την ίδια y συντεταγμένη τότε η πιο αριστερή πάνω στον χ άξονα έχει την μεγαλύτερη προτεραιότητα. 'Ετσι το επόμενο "γεγόνος" για επεξεργασία μπορεί να το βρει ο αλγόριθμος σε Ο(logn) χρόνο.
Κορυφή στρόφης καλούμε μια κορυφή του Π πάνω στην οποία η κατεύθυνση προς την οποία "περπατάμε" (από την πιο ψηλή στην πιο χαμηλή κορυφή κατά μήκος της α ριστέρης ή της δεξίας πλευράς του Π ) αλλάζει άπο "κατηφορική" σε "ανηφορική" ή αντίστροφα.
Μια κορυφή π είναι χαμηλότερα από μια κορυφή ρ αν ισχύει π.y < ρ.y ή ισχύει π.y = ρ.y και π.χ > ρ.χ.
Μια κορυφή ρ είναι ψηλότερα από μια κορυφή π αν ισχύει ρ.y > π.y ή ισχύει
ρ.y = π.y και ρ.χ < π.χ . ( Μπορούμε να φανταστούμε ότι περιστρέφουμε το Π ελαφρά δεξιόστροφα ως προς το σύστημα συντεταγμένων μας, έτσι ώστε δεν υπάρχει ζεύγος σημείων που να έχει την ίδια y συντεταγμένη. Η σχέχη "χαμηλότερα"/"ψηλότερα" που μόλις ορίσαμε είναι η ίδια με την "χαμηλότερα"/"ψηλότερα" σχέση στο ελαφρά στραμένο Π.
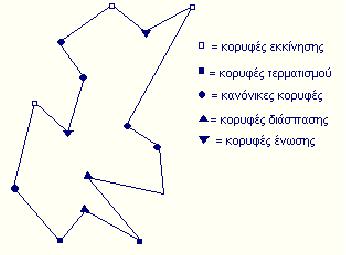
Κορυφή εκκίνησης καλούμε μια κορυφή κ του Π αν οι δυο γειτονικές της κόρυφες κείτονται χαμηλότερα της και η εσωτερική γώνια στη κ είναι μικρότερη άπο π. Αν η εσωτερίκη αυτή γωνία είναι μεγαλύτερη άπο π τότε η κ καλείται κορυφή διάσπασης.
Κορυφή τερμάτισμου καλούμε μια κορυφή κ του Π αν οι δυο γειτονικές της κόρυφες κείτονται ψηλότερα της και η εσωτερική γώνια στη κ είναι μικρότερη άπο π. Αν η εσωτερίκη αυτή γωνία είναι μεγαλύτερη άπο π τότε η κ καλείται κορυφή ένωσης.
Κανονική κορυφή καλούμε κορυφή κ του Π η οποία δεν είναι κόρυφη στροφής.
Ένα απλό πολύγωνο Π είναι y-μονότονο αν δεν έχει κορυφές διάσπασης και κορυφές ένωσης.
Το παραπάνω λήμμα υποδηλώνει ότι το Π θα έχει διαμεροστεί σε y-μονότονα κομμάτια όταν θά έχουμε απαλαχθεί από τις κορυφές διάσπαση και τις κορυφές ένωση . Αυτό το καταφέρνουμε προσθέτοντας μια διαγώνιο με κατεύθυνση προς τα πάνω άπο κάθε κορυφή διάσπασης και μια διαγώνιο με κατεύθυνση προς τα κάτω άπο κάθε κορυφή ένωσης. Αυτές οι διαγώνιοι δεν θα πρέπει να τέμνονται μεταξύ τους. Όταν θα έχουμε προσθέσει όλες τις διαγωνίους το Π θα έχει διασπαστεί σε y-μονότονα κομμάτια.
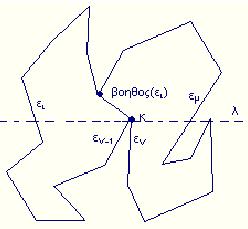
Ο στόχος τησ σάρωσης είναι να προσθέσει διαγωνίους άπο κάθε κορυφή διάσπασης σε μια κορυφή που βρίσκεται ψηλοτερά της. Ας υποθέσουμε οτι η γράμμη σάρωσης λ έχει φτάσει σε μια κορυφή διάσπασης κ. Με ποιά κορυφή πρέπει να συνδέσουμε την κ ; 'Εστω ει η ακμή αμμέσως στα αριστερά της κ πάνω στην λ, και έστω εκ η ακμή αμμέσως στα δεξία. Τότε μπορούμε να συνδέσουμε την κ με την χαμηλότερη κορυφή ανάμεσα στις ει και εκ και ψηλότερα της κ. Αν δεν υπάρχει τέτοια κορυφή τότε μπορούμε να συνδέσουμε την κ με το "πάνω" σήμειο της ει ή το πάνω σημείο της εκ. Σαν βοηθητική της ει -βοηθητική(ει)- ορίζουμε την χαμηλότερη κορυφή πάνω από την λ έτσι ώστε το οριζόντιο ευθύγραμμο τμήμα που συνδέει την κορυφή αυτή με την ει να κείτεται εντός του Π. Ας σημειωθεί ότι η βοηθητική(ει) μπόρει να είναι και το πάνω σημείο της ίδιας της ει. Άρα προκειμένου να απαλλαχθούμε από τις κορυφές διάσπασης τις συνδέουμε με την βοηθητική της ακμής αμμέσως στα αριστερά τους.
Φαίνεται πιο δύσκολο να απαλλαχθούμε από τις κορυφές ένωσης αφού
χρειάζονται μια κορυφή προς μια χαμηλότερη κορυφή. Αφού το μέρος του Π
που βρίσκεται κάτω από την λ δεν το έχουμε ερευνήσει ακόμα δεν μπορούμε
να προσθέσουμε μια τέτοια διαγώνιο οταν συναντάμε μια κορυφή ένωσης.
Όμως ας υποθέσουμε οτι η λ φτάνει σε μια κορυφή ένωσης κι. Έστω ει και εκ
οι ακμές αμμέσως στα αριστερά και στα δεξιά της κι πάνω στην λ.
Παρατηρούμε οτι η κι γίνεται η νέα βοηθητική της ει όταν φτάνουμε σε
αυτήν. Θα θέλαμε να συνδέσουμε την κι με την ψηλότερη κορυφή κάτω από την
γραμμή σάρωσης λ και ανάμεσα στις ει και εκ. Φυσικά δεν ξέρουμε την ψηλότερη
κορυφή κάτω από την λ όταν φτάνουμε στην κι. Αλλά είναι εύκολο να την βρούμε
αργότερα , όταν φτάνουμε μια κορύφη κμ που αντικαθιστά την κι σαν
βοηθητική της ει τότε αυτή είναι η κορυφή που ψάχναμε.
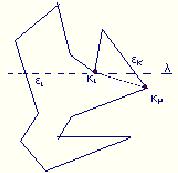
Άρα όποτε αντικαθιστούμε την βοηθητική μιας ακμής ,ελέγχουμε αν η παλιά βοηθητική είναι κορυφή ένωσης, και αν είναι τότε προσθέτουμε μια διαγώνιο ανάμεσα στην παλιά βοηθητική και την καινούργια. Αυτή η διαγώνιος προστίθεται πάντα όταν η νεα βοηθητική είναι κορυφή διάσπασης προκείμενου να απαλλαχτούμε από την κορυφή διάσπασης. Αν η παλιά βοηθητική ήταν κορυφή ένωσης τότε απαλλασόμαστε με μια διάγωνιο από μια κορυφή ένωσης και μια διάσπασης ταυτόχρονα. Μπορεί επίσης να συμβεί η βοηθητική της ει να μην αντικατασταθεί μετέπειτα κάτω από την κι. Σε αυτή την περίπτωση μπορούμε να συνδέσουμε την κι με το χαμηλότερο σημείο της ει.
Με την παραπάνω προσέγγιση χρειάζεται να βρούμε την ακμή στα αριστερά κάθε κορυφής. Γι'αυτό κρατάμε τις ακμές του Π που τέμνουν την γραμμή σάρωσης λ στους κόμβους ενος δυαδικού δένδρου αναζήτησης Τ. Μια LVR traversal του Τ μας δίνει τις ακμές απο τα αριστερά προς τα δεξιά. Επειδή μας ενδιαφέρουν μονάχα οι ακμές στα αριστερά κορυφών ένωσης και διάσπασης αποθηκεύουμε στο Τ μόνο τις ακμές εκείνες του Π που έχουν το Π στα δεξιά τους.
Με κάθε ακμή στο Τ κρατάμε και την βοηθητική της κορυφή. Το δένδρο Τ μαζί με τις βοηθητικές και τις ακμές αποτελούν την κατάσταση του αλγορίθμου. Η κατάσταση αυτή αλλάζει καθώς μετακινείται η λ. Ακμές σταματούν ή αρχίζουν να τέμνουν την λ και η βοηθητική μιας ακμής ίσως αλλάξει.
Ο αλγόριθμος χωρίζει το Π σε υποπολύγωνα που πρέπει να επεξεργαστούμε σε μετέπειτα στάδιο. Προκειμένου να έχουμε μια εύκολη πρόσβαση σε αυτά τα αποθηκεύουμε μαζί με τις νέες διαγωνίους που προσθέτουμε σε μια διπλά-συνδεδεμένη-λίστα Λ. Το Π αρχικά δίνεται στο applet σαν ένας πίνακας από σημεία οπότε τον μετατρέπουμε πριν αρχίσουμε να προσθέτουμε διαγωνίους στην λίστα Λ.
Άρα ο αλγόριθμος έχει ως εξής
ΔΙΑΣΠΑΣΗ_ΣΕ_ΜΟΝΟΤΟΝΑ(Π)
Είσοδος - Απλό πολύγωνο Π αποθηκευμένο σε μια διπλά-συνδεδεμένη λίστα Λ
Έξοδος - Διαμέρηση του Π σε μονότονα-υποπολύγωνα αποθηκευμένα στην Λ
1. Κατασκεύασε μια ουρά προτεραιότητας Q με τις κορυφές του Π
χρησημοποιώντας την y-συντατεγμένη τους σαν προτεραιότητα.
2. Αρχικοποίησε ένα κενό δυαδικό δένδρο αναζήτησης Τ
3. Εφόσον Q δεν ειναι άδεια {
4. Αφαίρεσε την κορυφή κι με την μεγαλυτέρη προτεραιότητα απο την Q
5. Κάλεσε την ανάλογη διαδικασία να χειριστεί την κι ανάλογα με τον τύπο της .
}
ΧΕΙΡΙΣΜΟΣ_ΚΟΡΥΦΗΣ_ΕΚΚΙΝΗΣΗΣ(κι)
1. Εισήγαγε ει στο Τ και θέσε την βοηθητική(ει) = κι .
ΧΕΙΡΙΣΜΟΣ_ΚΟΡΥΦΗΣ_ΤΕΡΜΑΤΙΣΜΟΥ(κι)
1. Αν βοηθητική(ει-1) είναι κορυφή ένωσης
2. τοτε Εισήγαγε την διαγώνιο που συνδέει την κι με την βοηθητική(ει-1) στην Λ
3. Σβήσε την ει-1 από το Τ
ΧΕΙΡΙΣΜΟΣ_ΚΟΡΥΦΗΣ_ΕΝΩΣΗΣ(κι)
1. Αν βοηθητική(ει-1) είναι κορυφή ένωσης
2. τότε Εισήγαγε τη διαγώνιο που συνδέει την κι με τη βοηθητική(ει-1) στην Λ
3. Σβήσε την ει-1 από το Τ
4. Ψάξε στο Τ να βρεις την ακμή εj ακρίβως στα αριστερά της κι
5. Αν βοηθητική(εj) είναι κορυφή ένωσης
6. τοτε Εισήγαγε τη διαγώνιο που συνδέει την κι με τη βοηθητική(εj) στην Λ
7. Βοηθητική(εj) = κι
ΧΕΙΡΙΣΜΟΣ_ΚΟΡΥΦΗΣ_ΔΙΑΣΠΑΣΗΣ(κι)
1. Ψάξε στο Τ να βρεις την ακμή εj ακρίβως στα αριστερά της κι
2. Εισήγαγε τη διαγώνιο που συνδέει την κι με τη βοηθητική(εj) στην Λ
3. Βοηθητική(εj) = κι
4. Εισήγαγε ει στο Τ και θέσε τη βοηθητική(ει) = κι .
ΧΕΙΡΙΣΜΟΣ_ΚΟΡΥΦΗΣ_ΚΑΝΟΝΙΚΗΣ(κι)
1. Αν το εσωτερίκο του Π κείτεται στα αριστερά της κι
2. τότε Αν βοηθητική(ει-1) είναι κορυφή ένωσης
3. τότε Εισήγαγε τη διαγώνιο που συνδέει την κι με τη
βοηθητική (ει-1) στην Λ.
4. Σβήσε την ει-1 από το Τ .
5. Εισήγαγε ει στο Τ και θέσε την βοηθητική(ει) = κι .
6. αλλοιώς Ψάξε στο Τ να βρεις την ακμή εj ακρίβως στα αριστερά της κι
7. Αν βοηθητική(εj) είναι κορυφή ένωσης
8. τότε Εισήγαγε τη διαγώνιο που συνδέει την κι με τη
βοηθητική(εj) στην Λ
9. βοηθητική(εj) = κι.
Έστω Π ένα y-μονότονο πολύγωνο με ν κορυφές.
Ο αλγόριθμος χειρίζεται τις κορυφές με σειρά φθίνουσης y-συντεταγμένης.
Αν δυο κορυφές έχουν την ίδια y-συντεταγμένη , τότε η ποιό αριστερή
είναι αυτή που χειρίζεται πρώτα ο αλγόριθμος.
Ο αλγόριθμος απαιτεί μια στοίβα Σ σαν βοηθητική δομή δεδομένων στην
οποία επιτελούμε τις λειτουργίες "βάλε"(push) ,"βγάλε"(pop).
Αρχικά η Σ είναι άδεια , αργότερα περιέχει τις κορυφές του Π που έχουμε συναντήσει , οι οποίες όμως ίσως χρειάζονται περισσότερες διαγωνίους. Όποτε χειριζόμαστε
μια κορυφή προσθέτοτυμε όσο το δυνατό περοσσότερες διαγωνίους
από αυτήν την κορυφή σε κορυφές που είναι στην στοίβα. Οι διαγώνιοι
"κόβουν" τρίγωνα από το Π. Οι κορυφές τις οποίες έχουμε χειριστεί
αλλά δεν τις έχουμε "κόψει"(οι κορυφές που είναι δηλαδή στην στοίβα)
είναι στο σύνορο του μέρους του Π που χρειάζεται ακόμα
να τριγωνοποιηθεί. Η χαμηλότερη από τις κορυφές , η οποία είναι αυτή
που έχουμε συναντήσει τελευταία, είναι στην κορυφή της στοίβας , η
δεύτερη χαμηλότερη είναι δεύτερη στην στοίβα κοκ.
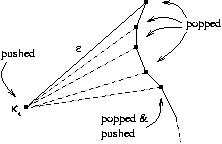
Το μέρος του Π που χρειάζεται ακόμα να τριγωνοποιηθεί και βρίσκεται πάνω από την τελευταία κορυφή που έχει συναντήσει ο αλγόριθμος μέχρι τώρα, έχει ένα συγκεκριμένο σχήμα, μοιάζει σαν αναποδυρισμένο χωνί. Μια πλευρά αυτού του χωνιού αποτελείται από το μέρος μιας ακμής του Π, και η άλλη πλευρά είναι μια αλυσίδα από κορυφές(μη κυρτές) των οποίων η εσωτερική γωνία είναι τουλάχιστον 180 μοίρες, Μόνο η ψηλότερη κορυφή , που είναι στον πάτο της στοίβας έχει εσωτερική γωνία μικρότερη των 180 μοιρών (κύρτη). Αυτή η ιδιότητα παραμένει αληθής ακόμα και μετά τον χειρισμό της επόμενης κορυφής. Δηλαδή αποτελεί αναλλοίωτη συνθήκη του αλγορίθμου.
Τώρα ας δούμε ποιές διαγωνίους μπορούμε να προσθέσουμε όταν χειριζόμαστε την επόμενη κορυφή. Πρέπει καταρχάς να διακρίνουμε δυο περιπτώσεις . α) η κι , η επόμενη κορυφή , βρίσκεται στην ίδια πλεύρα με τις μη κυρτές κορυφές που είναι στην στοίβα, ή β) βρίσκεται στην αντίθετη πλευρά.
α) Αν η κι βρίσκεται στην αντίθετη πλευρά τότε πρέπει να είναι
το χαμηλότερο σημείο μιας μόνο ακμής ε που είναι και πλευρά του χωνιού.
Εξαιτίας του σχήματος του χωνιού μπορούμε να προσθέσουμε διαγωνίους από
την κι σε όλες τις κορυφές που βρίσκονται την δεδομένη στιγμή στην στοίβα
, εκτός από την τελευταία (αφού η τελευταία κορυφή της στοίβας είναι η
πάνω κορυφή της ε , και άρα είναι ήδη συνδεδεμένη με την κι .
Όλες αυτές οι κορυφές αφαιρούνται από την στοίβα. Το μέρος του Π
που δεν έχει ακόμα τριγωνοποιηθεί που βρίσκεται πάνω από την κι
είναι φραγμένο από την διαγώνιο που συνδέει την κι με την κορυφή
που προηγουμένος ήταν στην κορυφή της στοίβας και από την ακμή
του Π που εκτείνεται προς τα κάτω από αυτήν την κορυφή , έτσι
μοιάζει σαν χωνί και η αναλλοίωτη διατηρείται. Αυτή η κορυφή
και η κι παραμένουν μέρος του μέρους του Π που δεν έχει ακόμα τριγωνοποιηθεί
και γι'αυτό ξαναμπαίνουν στη στοίβα.
β) Η άλλη περίπτωση είναι η κι να βρίσκεται στην ίδια πλευρά
με τις μη-κυρτές κορυφές τις στοίβας. Αυτήν την φορά ίσως να μην
μπορούμε να ζωγραφίσουμε διαγωνίους από την κι προς όλες τις κορυφές
στην στοίβα. Παρολαυτά αυτές με τις οποίες μπορούμε να συνδέσουμε την
κι είναι όλες διαδοχικές και βρίσκονται στην κορυφή της στοίβας, άρα
μπορούμε να προχωρήσουμε ως εξής . Πρώτα αφαιρούμε μια κορυφή από την
στοίβα, αυτή η κορυφή είναι ήδη συνδεδεμένη με την κι με μια ακμή του Π.
Μετά αφαιρούμε κορυφές από την στοίβα και τις συνδέουμε
με την κι μέχρι να συναντήσουμε μια όπου αυτό είναι αδύνατο.
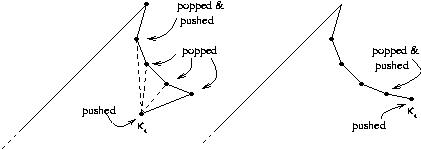
Το να ελέγξουμε αν μια διαγώνιος μπορεί να ζωγραφιστεί από την κι σε μια κορυφή κλ που είναι στην στοίβα μπορεί να γίνει κοιτώντας στις κι και κλ και στην προηγούμενη κορυφή που αφαιρέθηκε απο την στοίβα. Όταν βρούμε μια κορυφή με την οποία δεν μπορούμε να συνδέσουμε την κι τοτε βάζουμε την τελευταία κορυφή, η οποία είχε αφαιρεθεί από την στοίβα, πίσω στην στοίβα. Αυτή είναι είτε η τελευταία κορυφή με την οποία είχε συνδεθεί διαγώνιος , ή (άμα δεν προστέθηκε διαγώνιος) είναι η γειτονική της κι στην πλευρά του Π(δες σχήμα). Αφού το κάναμε αυτό βάζουμε την κι στην στοίβα. Και στις δυο περιπτώσεις η αναλλοίωτη συνθήκη διατηρείται : μια πλευρά του χωνιού αποτελείται από ένα μέρος μιας ακμής του Π ,και η άλλη πλευρά αποτελείται από μια αλυσίδα από μη-κυρτές κορυφές.
Αλγόριθμος
ΤΡΙΓΩΝΟΠΟΙΗΣΗ_ΜΟΝΟΤΟΝΟΥ_ΠΟΛΥΓΩΝΟΥ(Π) είσοδος: Ένα y-μονότονο πολύγωνο Π αποθηκευμένο σε μια διπλά-συνδεδεμένη λίστα Λ έξοδος: Μια τριγωνοποίηση του Π αποθηκευμένη στην Λ 1. Συγχώνευσε τις κόρυφες στην αριστερή και στην δεξιά πλευρά του Π σε μια ακολουθία , ταξινομημένη με φθίνουσα την y-συντεταγμένη. Αν δυο κορυφές έχουν την ίδια y-συντεταγμένη, τότε η πιο αριστέρη έρχεται πρώτη. Έστω κ1,κ2,...,κν η ταξινομημένη ακολουθία. 2. Βάλε τις κ1 και κ2 στην στοίβα Σ. 3. Για ι = 3 μέχρι ι = ν-1 { 4. Αν κι και η κορυφή στην κορυφή της Σ είναι σε διαφορετικές πλευρές 5. τότε Αφαίρεσε όλες τις κορυφές από την Σ. 6. Βάλε στην Λ ,διαγώνιο από την κι προς κάθε κορυφή που έβγαλες , εκτός της τελευταίας. 7. Βάλε την κι-1 στην Σ 8. αλλιώς Βγάλε μια κορυφή από την Σ 9. Βγάλε τις άλλες κορυφές από την Σ εφόσον οι διαγώνιοι από την κι προς αυτές είναι εντός του Π. Βάλε αυτές τις διαγώνιους στην Λ. Βάλε την τελευταία κορυφή που αφαιρέθηκε από την Σ πίσω σε αυτήν. 10. Βάλε την κι στην Σ 11. Πρόσθεσε διαγωνίους από την κν προς όλες τις κορυφές της Σ εκτός της πρώτης και της τελευταίας.
Βιβλιογραφεία :
Computational Geometry , M.de Berg, M.van Kreveld, M. Overmars, O.Schwarzkopf Springer.